参考:代码随想录回溯算法
组合问题
待选组合无重复元素
待选组合无重复元素,但可以多次选取同样的元素
待选组合有重复元素,且待选元素只可以被使用一次
组合问题
一般是给定一个集合和特定要求,求有多少种子集合能符合特定要求。
需要合理暴力才能在规定时间内完成算法,如果只是n个for循环再加时间不限,确实是可以满足要求,但咱作为有追求的coder是不允许自己写出那种代码的。
待选组合无重复元素

借用卡哥的图来翻译翻译

给定一个集合,从中取出有限个个数,且不能重复选取
有点类似于取球游戏
第一次取出的球,不放回去,再拿剩下的n个,均不放回。
取完记录下来,将除了第一次取出的球全部放回,循环往复记录结果
不同的是,数组中的元素是有序的,为了不漏掉每一种结果,可以使用循环的方式来实现这个过程
代码:
//结果集合
List<List<Integer>> res = new ArrayList<>();
//路径集合
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combine( int n, int k ) {
// 从n个数中选取 k 个数, 从 1 开始
show( n, k, 1 );
return res;
}
private void show( int n, int k, int start ) {
// 收集到了k 个数,res 记录
if ( path.size() == k ) {
printIndent( count );
System.out.println( "进入收集,第" + count + "层 ,收集到结果=" + path.toString() );
res.add( new ArrayList<>( path ) );
return;
}
// 从 start 开始,再选 x 个数,x 取决于之前选取了几个数
for ( int i = start; i <= n; i++ ) {
printIndent( count++ );
System.out.println( "i=" + i + "第" + count + "层 ,回溯前=" + path.toString() );
// 新的数加入到集合中
path.add( i );
// 从下一个数开始选择,直到 当前 path 收集到了k个数
show( n, k, i + 1 );
//将上一个加入的数剔除,从下一个数继续执行选择。
path.removeLast();
printIndent( --count );
System.out.println( "i=" + i + "第" + count + "层 ,回溯后=" + path.toString() );
}
}
// 全局变量,记录递归函数的递归层数
int count = 0;
// 输入 n,打印 n 个 tab 缩进
void printIndent( int n ) {
for ( int i = 0; i < n; i++ ) {
System.out.printf( " " );
}
}
通过打印中间的递归函数调用过程,可以更好的理解整个回溯过程
i=1第1层 ,回溯前=[1]
i=2第2层 ,回溯前=[1, 2]
进入收集,第2层 ,收集到结果=[1, 2]
i=2第1层 ,回溯后=[1]
i=3第2层 ,回溯前=[1, 3]
进入收集,第2层 ,收集到结果=[1, 3]
i=3第1层 ,回溯后=[1]
i=4第2层 ,回溯前=[1, 4]
进入收集,第2层 ,收集到结果=[1, 4]
i=4第1层 ,回溯后=[1]
i=1第0层 ,回溯后=[]
i=2第1层 ,回溯前=[2]
i=3第2层 ,回溯前=[2, 3]
进入收集,第2层 ,收集到结果=[2, 3]
i=3第1层 ,回溯后=[2]
i=4第2层 ,回溯前=[2, 4]
进入收集,第2层 ,收集到结果=[2, 4]
i=4第1层 ,回溯后=[2]
i=2第0层 ,回溯后=[]
i=3第1层 ,回溯前=[3]
i=4第2层 ,回溯前=[3, 4]
进入收集,第2层 ,收集到结果=[3, 4]
i=4第1层 ,回溯后=[3]
i=3第0层 ,回溯后=[]
i=4第1层 ,回溯前=[4]
i=4第0层 ,回溯后=[]
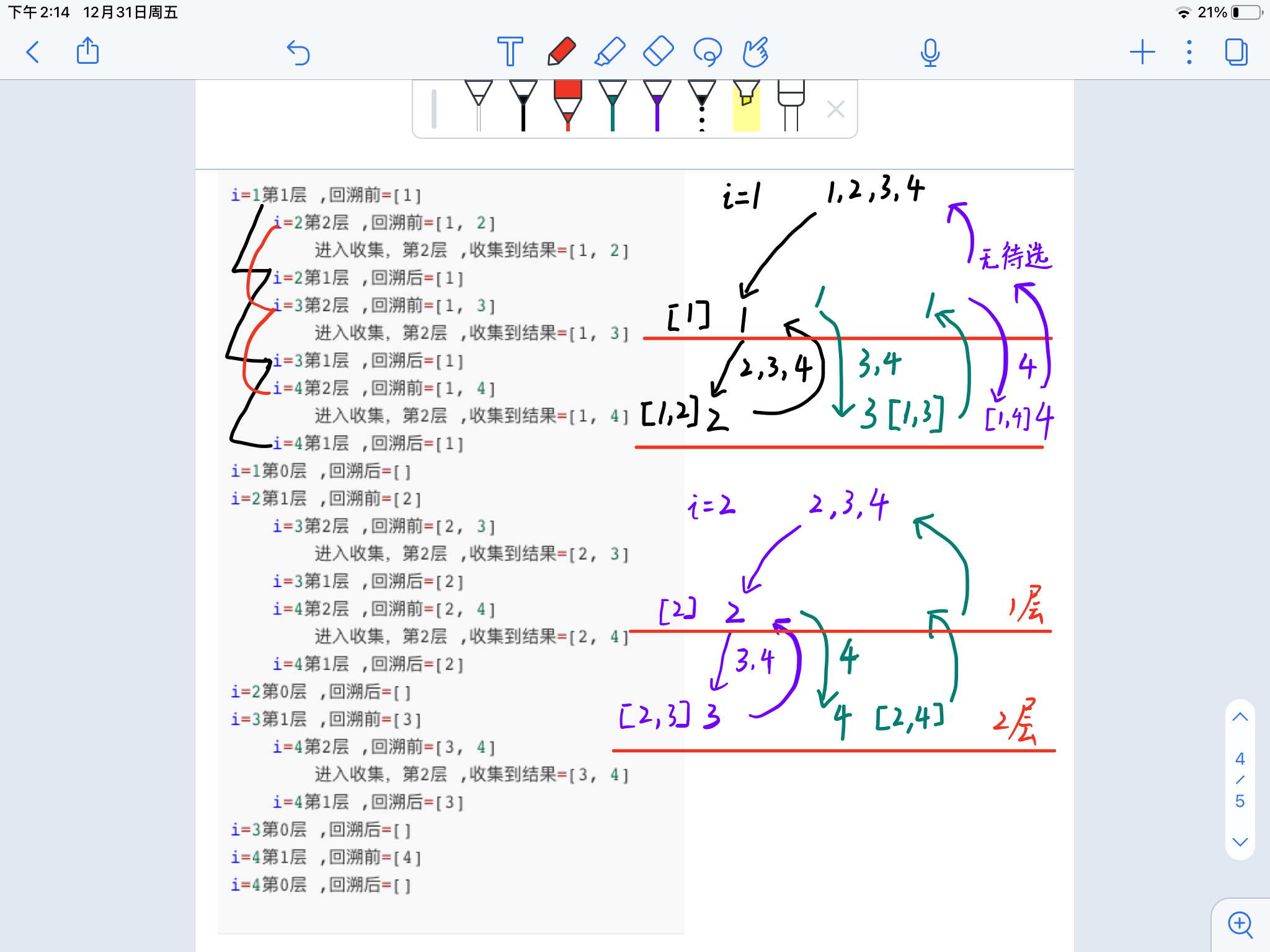
例子: 1,2,3,4。 选2个数组合
i = 1 时,第一个数是 1 , 只能从剩下的 2,3,4 中选。
先选 2 , 收集到了 2 个数,记录res.add(【1,2】)
然后回溯到开始选择之前,path集合中只有【1】
i = 3 ,选择 3 ,收集到了 2个数,记录【1,3】
回溯,path集合为【1】
i = 4 ,选择 4 ,收集到了 2个数,记录【1,4】
回溯,path集合为【1】
i == 4 退出循环,再次回溯
path 集合 【】
i = 2 ,第一个数是 2 , 只能从剩下的 3,4 中选。
然后过程与上面类似

和上一个题类似,只不过结果条件变成了集合中的数需要等于某个数,且子集合的元素不能重复选取
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
int sum = 0;
int end = 9;
public List<List<Integer>> combinationSum3( int k, int n ) {
show( k, n, 1 );
return res;
}
private void show( int k, int n, int start ) {
//System.out.println(n+"--"+sum +" "+ k+"--"+ path.size());
if ( path.size() == k && sum == n ) {
//printIndent( count );
//System.out.println( "进入收集,第" + count + "层 ,收集到结果=" + path.toString() );
res.add( new ArrayList<>( path ) );
return;
} else if ( sum > n ) {
return;
}
for ( int i = start; i <= end; i++ ) {
if ( path.contains( i ) ) {
continue;
}
path.add( i );
sum = sum + i;
//printIndent( count++ );
//System.out.println( "i=" + i + "第" + count + "层 ,回溯前=" + path.toString() + "sum="+sum);
show( k, n, i + 1 );
path.removeLast();
sum = sum - i;
printIndent( --count );
//System.out.println( "i=" + i + "第" + count + "层 ,回溯后=" + path.toString() );
}
}
// 全局变量,记录递归函数的递归层数
int count = 0;
// 输入 n,打印 n 个 tab 缩进
void printIndent( int n ) {
for ( int i = 0; i < n; i++ ) {
System.out.printf( " " );
}
}
//设置全局列表存储最后的结果
List<String> list = new ArrayList<>();
public List<String> letterCombinations(String digits) {
if (digits == null || digits.length() == 0) {
return list;
}
//初始对应所有的数字,为了直接对应2-9,新增了两个无效的字符串""
String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
//迭代处理
backTracking(digits, numString, 0);
return list;
}
//每次迭代获取一个字符串,所以会设计大量的字符串拼接,所以这里选择更为高效的 StringBuild
StringBuilder temp = new StringBuilder();
//比如digits如果为"23",num 为0,则str表示2对应的 abc
public void backTracking(String digits, String[] numString, int num) {
//遍历全部一次记录一次得到的字符串
if (num == digits.length()) {
list.add(temp.toString());
return;
}
//str 表示当前num对应的字符串
String str = numString[digits.charAt(num) - '0'];
for (int i = 0; i < str.length(); i++) {
temp.append(str.charAt(i));
//c
backTracking(digits, numString, num + 1);
//剔除末尾的继续尝试
temp.deleteCharAt(temp.length() - 1);
}
}
待选组合无重复元素,但可以多次选取同样的元素

和 216. 组合总和 III 不同的是,这次可以在集合中重复选取某个元素,其集合中的元素值是唯一的。
建议自己思考如何实现子集合在回溯过程中,重复选取一个元素
代码中有答案
class Solution {
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
int sum = 0;
// 全局变量,记录递归函数的递归层数
int count = 0;
// 输入 n,打印 n 个 tab 缩进
void printIndent( int n ) {
for ( int i = 0; i < n; i++ ) {
System.out.printf( " " );
}
}
public List<List<Integer>> combinationSum( int[] candidates, int target ) {
getCombination(candidates,target,0);
return res;
}
private void getCombination( int[] candidates, int target,int start) {
if(sum>target)return;
if(sum==target){
//System.out.println( "进入收集,第" + count + "层 ,收集到结果=" + path.toString() );
res.add(new ArrayList<>(path));
return;
}
for(int i=start;i<candidates.length;i++){
sum+=candidates[i];
path.add( candidates[i] );
// printIndent( count++ );
// System.out.println( "i=" + i + "第" + count + "层 ,回溯前=" + path.toString() + "sum="+sum);
// 此处从 i 位置出发,代表当前子集合还可以再次选取 这个元素
getCombination( candidates,target,i );
sum-=candidates[i];
path.removeLast();
// printIndent( --count );
// System.out.println( "i=" + i + "第" + count + "层 ,回溯后=" + path.toString() );
}
}
}
待选组合有重复元素,且待选元素只可以被使用一次
40. 组合总和 II

这次要求,在可能含有重复元素的集合中,找出子集合之和为target,且集合内的元素只能使用一次 的 所有不重复的子集合
如果按照之前的办法,直接回溯,结果集中会包含重复的集合
比如 【1,2(a),2(b),2(c),5】 target
此处用a\b\c来代表标记重复元素
正确解集应该是 【【1,2(a、b、c),2(除了前一个元素的认一个)】,【5】】
但如果直接回溯,会出现【1,2,2】、【1,2,2】、【1,2,2】三个相同的解集
这是因为在回溯过程中,尽管不同的2 值一样,但他们在集合的位置中是不同的,上面的回溯代码无法处理,相同值不同位置的情况 , 也就出现了看起来是一样的子集合
图来自代码随想录回溯部分
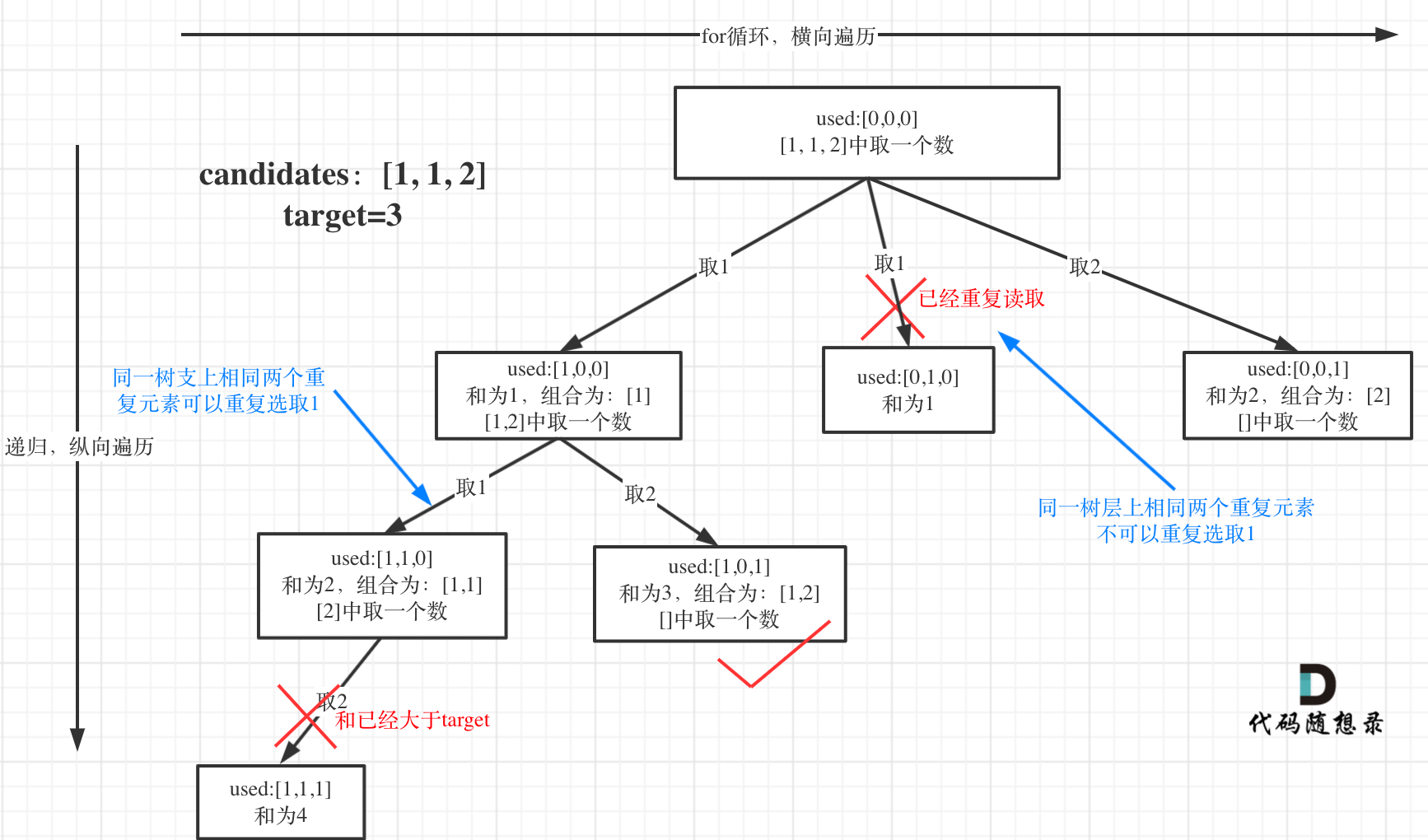
所以本题的重点在于,如何在回溯过程中, 不使用之前正确集合中使用过的值 ,且完成所有解集的搜集。
可以使用一个标记数组,来判断这个数字是否使用过,先对给定集合数组排序,然后建立对应的标记数组。
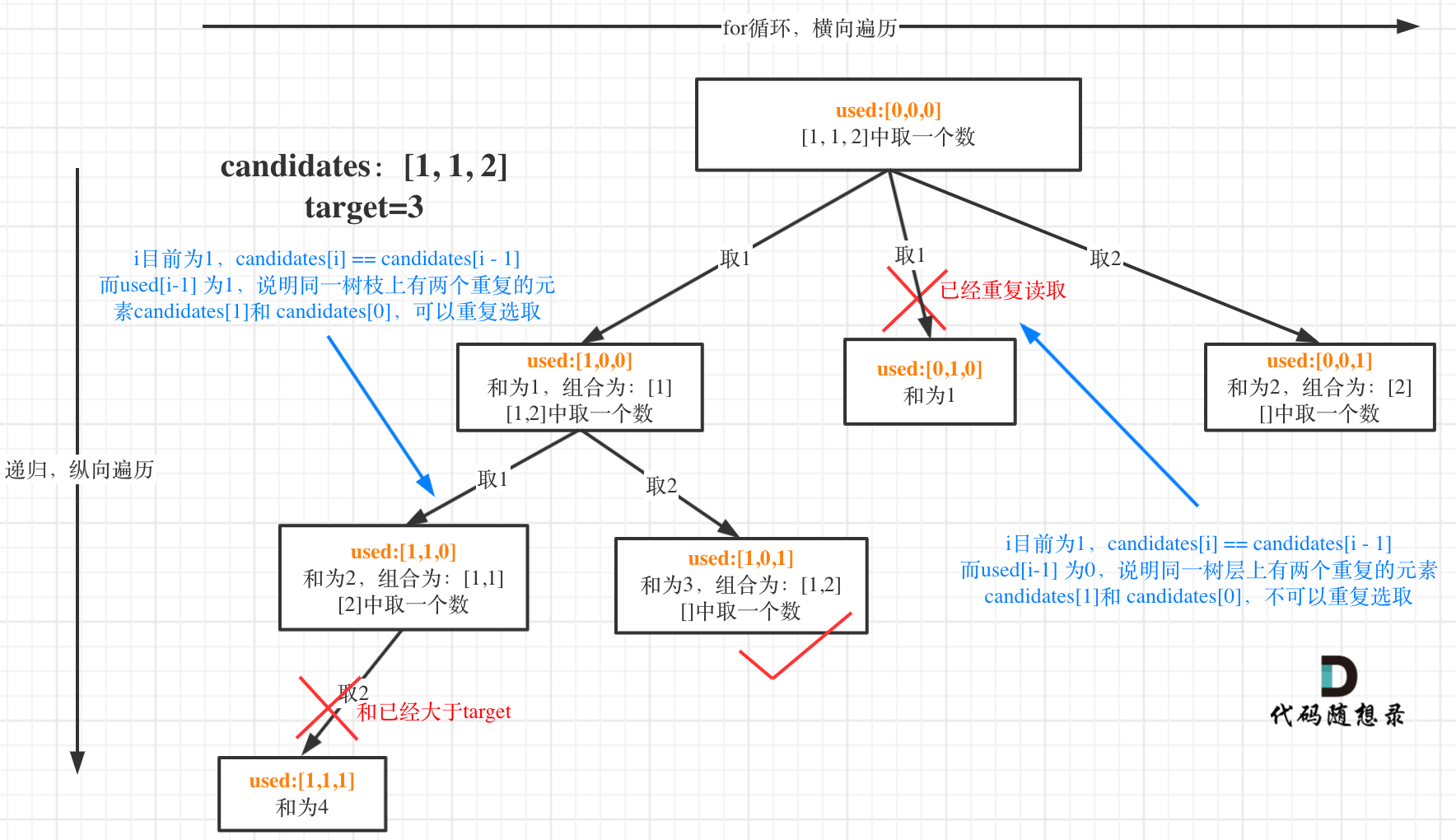
去重操作应该为:
如果当前path集合中,新选取的元素和上一个选取的元素是一样的,且之前的解集集合中使用过了当前元素, 那就跳过
对应到代码就是
candidates[i] == candidates[i - 1] //新选取的元素和上一个元素一样
&&
used[i - 1] == false // 之前解集集合使用过当前元素
class Solution {
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort( candidates );
boolean []used = new boolean[candidates.length];
getCombination(candidates,used,target,0);
return res;
}
int sum =0;
private void getCombination( int[] candidates, boolean[] used,int target,int start ) {
if(sum>target)return;
if(sum==target){
res.add(new ArrayList<>(path));
return;
}
for(int i=start;i<candidates.length;i++){
//只能剔除第一位重复 题目要求是每一位开头只求一次
//if(path.size()==0 && i>0 && candidates[i]==candidates[i-1])continue;
// 相当于把重复元素值的解给剔除了
//if(path.size()>0 && path.getLast()==candidates[i])continue;
//正确剔除重复解的办法
if(i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]){
continue;
}
used[i]=true;
sum+=candidates[i];
path.add(candidates[i]);
getCombination(candidates,used,target,i+1);
used[i]=false;
int temp = path.getLast();
sum-=temp;
path.removeLast();
}
}
}
不使用标记数组的办法:
上面的办法中,去重要求
i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]
递归为:
getCombination(candidates,used,target,i+1);
其实当 i > start 时,它新选择的元素已经不会是之前选择过的元素,所以可以不使用标记数组
class Solution {
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
int sum = 0;
public List<List<Integer>> combinationSum2( int[] candidates, int target ) {
//为了将重复的数字都放到一起,所以先进行排序
Arrays.sort( candidates );
backTracking( candidates, target, 0 );
return res;
}
private void backTracking( int[] candidates, int target, int start ) {
if ( sum == target ) {
res.add( new ArrayList<>( path ) );
return;
}
for ( int i = start; i < candidates.length && sum + candidates[i] <= target; i++ ) {
//正确剔除重复解的办法
//跳过同一树层使用过的元素
if ( i > start && candidates[i] == candidates[i - 1] ) {
continue;
}
sum += candidates[i];
path.add( candidates[i] );
// i+1 代表当前组内元素只选取一次
backTracking( candidates, target, i + 1 );
int temp = path.getLast();
sum -= temp;
path.removeLast();
}
}
}
