暴力递归到动态规划
题目---》找到暴力递归写法(尝试)
---》把可变参数,不讲究组织的形式,做缓存,那就是记忆化搜索的方法(拥有重复解的前提下)
---》精细化组织----》那就是动态规划
如果暴力过程中没有枚举行为(即通过循环来求得值)
则记忆化搜索和动态规划的时间复杂度一致,没有必要从记忆化搜索再优化为动态规划
什么暴力递归可以继续优化?
有重复调用同一个子问题的解,这种递归可以优化
如果每一个子问题都是不同的解,无法优化也不用优化
暴力递归和动态规划的关系
某一个暴力递归,有解的重复调用,就可以把这个暴力递归优化成动态规划
任何动态规划问题,都一定对应着某-个有解的重复调用的暴力递归
但不是所有的暴力递归,都一定对应着动态规划
面试题和动态规划的关系
解决一个问题,可能有很多尝试方法
可能在很多尝试方法中,又有若干个尝试方法有动态规划的方式
一个问题可能有若干种动态规划的解法
如何找到某个问题的动态规划方式?
1)设计暴力递归:重要原则+4种常见尝试模型!重点!
2)分析有没有重复解:套路解决
3)用记忆化搜索->用严格表结构实现动态规划:套路解决
4)看看能否继续优化:套路解决
面试中设计暴力递归过程的原则
1)每一个可变参数的类型,一定不要比int类型更加复杂
2)原则1)可以违反,让类型突破到一维线性结构,那必须是唯一-可变参数
3)如果发现原则1)被违反,但不违反原则2),只需要做到记忆化搜索即可
4)可变参数的个数,能少则少
常见的4种尝试模型
1)从左往右的尝试模型.
2)范围上的尝试模型
3)多样本位置全对应的尝试模型
4)寻找业务限制的尝试模型
机器人路线问题
假设有排成-行的N个位置,记为1~N, N一定大于或等于2
开始时机器人在其中的M位置上(M -定是1~N中的一个)
如果机器人来到1位置,那么下一步只能往右来到2位置;
如果机器人来到N位置,那么下一步只能往左来到N-1位置;
如果机器人来到中间位置,那么下一步可以往左走或者往右走;
规定机器人必须走K步,最终能来到P位置(P也是1 ~N中的一个)的方法有多少种
给定四个参数N、M、K、P,返回方法数。
暴力递归
public static int ways1(int N, int M, int K, int P) {
//参数无效直接返回0
if(N<2||K<1||M<1||M>N||P<1||P>N) {
return 0;
}
//总共N个位置,从M点出发,还剩K步,返回最终能达到P的方法数
return walk(N, M, K, P);
}
//N:位置为1~N,固定参数
// cur :当前在cur位置,可变参数
// rest :还剩res步没有走,可变参数
// P :最终目标位置是P,固定参数
//该函数的含义:只能在1~N这些位置上移动,当前在cur位置,走完rest步之后, 停在P位置的方注
public static int walk(int N, int cur, int rest, int P) {
//如果没有剩余步数了,当前的cur位置就是最后的位置
//如果最后的位置停在P上,那么之前做的移动是有效的
//如果最后的位置没在P上,那么之前做的移动是无效的
if (rest == 0) {
returncur==P?1:0;
}
//如果还有rest步要走,而当前的cur位置在1位置上,那么当前这步只能从1走向2
//后续的过程就是,来到2位置上,还剩rest-1步要走
if(cur==1){
return walk(N, 2, rest - 1, P);
}
//如果还有rest步要走,而当前的cur位置在N位置上,那么当前这步只能从N走向N-1
//后续的过程就是,来到N-1位置 上,还剩rest-1步 要走
if(cur==N){
return walk(N, N .1, rest - 1, P);
}
//如果还有rest步要走,而当前的cur位置在中间位置上,那么当前这步可以走向左,也可以走
//走向左之后,后续的过程就是,来到cur-1位置上,还剩rest-1步要走
//走向右之后,后续的过程就是,来到cur+1位置 上,还剩rest-1步要走
//走向左、走向右是截然不同的方法,所以总方法数要都算上
return walk(N, cur + 1, rest - 1, P) + walk(N, cur - 1, rest - 1, P);
}
动态规划
public static int waysCache(int N, int M, int K, int P) {
//多数无效直接返间0
if (N<2||K<1||M<1||M>N||P<1||P>N){
return 0;
}
int[][] dp = new int [N+1][K+1];
for(int row = 0; row <= N; row++) {
for(int col = 0; col <= K; col++) {
dp[row][co1] = -1;
}
}
return walkCache(N, M, K, P,dp);
}
//我想把所ficur和lrest的组合,脑间的结果,加入到成存电
public static int walkCache(int N,int cur, int rest, int P, int[][] dp) {
if(dp[cur][rest] != -1) {
return dp[cur][rest];
}
if (rest == 0) {
dp[cur][rest] = cur==P?1: 0;
return dp[cur][rest];
}
if (cur== 1) {
dp[cur][rest] = walkCache(N, 2, rest - 1, P, dp);
return dp[cur][rest];
}
if (cur= N) {
dp[cur][rest] =walkCache(N, N - 1, rest .1, P,dp);
return dp[cur][rest];
}
dp[cur][rest] = walkCache(N, cur + 1, rest - 1, P,dp)
+ waLkCache(N, cur - 1, rest - 1, P, dp);
return dp[cur][rest];
}
计划搜索
动态规划 = 暴力递归+缓存
背包问题递归到动态规划
public static int dpWay(int[] W, int[] V, int bag) {
int N = W. length;
int[][] dp = new int[N + 1][bag + 1];
// dp[N][...] = 0
for (int index = N - 1; index >= 0; index--) {
for (int rest = 0; rest <= bag; rest++) { // rest < 0
int p1 = dp[index+1][rest];
int p2 = -1;
if(rest - w[index] >= 0) {
p2 = v[index] + dp[index + 1][rest - w[index]];
}
// dp[index][rest] = Math. max(p1, p2);
// int p1 = process(W,V, index + 1,rest);
// int p2 = -1;
//int p2Next = process(w, v, index + 1, rest - w[index]);
// if(p2Next != -1) {
// p2 = v[index] + p2Next;
// return Math. max(p1,p2);
}
}
return dp[e][bag];
}
字符串转化问题递归到动态规划
原方法:
public static int number(String str) {
if (str == null II str.1ength() == 0) {
return 0;
}
return process(str .toCharArray(), 0);
}
// str[0...i-1]已经转化定了, 固定川
// i之z前的他置, 如何转化已经做过决定了,不用脚关心
// i...们名少种转化的结果.
public static int process(char[] str, int i) {
if (i == str.length) { // base case
return 1;
}
// i没有到终止位置
if (str[i] == '0') {
return 0;
}
// str[i]字符不足‘日’
if (str[i] == '1') {
int res = process(str, i + 1); //自己作为单独的部分。后续有名少种方法
if (i + 1<str.1ength) {
res += process(str, i + 2); //1 (i和i+1)作为单独的部分。后续有名少种方法
}
return res;
}
if (str[i] == '2') {
int res = process(str, i + 1); // ii已作为单独的部分。后续有多少神方法
// (i利1+1)作为单独的部分并扎没有超:26.行使有名少种万法
// (1和i+1)作为单独的部分非且没有超上26.看续有名少种为法
if (i + 1< str.1ength && (str[i + 1] >= '0' && str[i + 1] <= '6')) {
res += process(str, i + 2); // (i和1+1)作:为单独的部分,i续有名少种方法
}
return res;
}
// str[i] == '3’~ '9' 3_ 无法转换
return process(str, i + 1);
}
动态规划
public static int number(String str) {
if (str == null II str.1ength() == 0) {
return 0;
}
return process(str .toCharArray(), 0);
}
// 一个可变参数 ,一维表
public static int process(char[] s, int i) {
if (str == null II str.1ength() == 0) {
return 0;
}
char[] str =s.toCharArray();
int N =str.length;
int []dp=new int[N+1];
//if (i == str.length) {
// dp[i]=1;
// }
dp[N]=1;
//因为暴力递归过程中,dp[i] 只依赖于 dp[i+1] dp[i+1]的位置,且dp[N] 已经固定为1
//所以是从右至左的模型
for(int i=N-1;i>=0;i--){
if (str[i] == '0') {
//return 0;
dp[i]=0;
}
if (str[i] == '1') {
//int res = process(str, i + 1); //自己作为单独的部分。后续有名少种方法
dp[i]=dp[i+1];
if (i + 1<str.1ength) {
//res += process(str, i + 2); //1 (i和i+1)作为单独的部分。后续有名少种方法
dp[i]+=dp[i+2];
}
//return res;
}
if (str[i] == '2') {
//int res = process(str, i + 1); // ii已作为单独的部分。后续有多少神方法
dp[i]=dp[i+1];
// (i利1+1)作为单独的部分并扎没有超:26.行使有名少种万法
// (1和i+1)作为单独的部分非且没有超上26.看续有名少种为法
if (i + 1< str.1ength && (str[i + 1] >= '0' && str[i + 1] <= '6')) {
//res += process(str, i + 2); // (i和1+1)作:为单独的部分,i续有名少种方法
dp[i]=dp[i+2];
}
//return res;
}
}
//return process(str .toCharArray(), 0);
return dp[0];
}
拿牌问题递归到动态规划
范围上的模型
暴力递归
public static int win1(int[] arr) {
if (arr == nu11|I arr.length == 0) {
return 0;
}
return Math . max(f(arr,0, arr.length - 1), s(arr, 0, arr .1ength - 1));
}
//先手
public static int f(int[] arr, int L, int R) {
if(L==R){
return arr[4];
}
return Math. max(
arr[L]+ s(arr, L + 1, R),arr[R] + s(arr, L, R - 1));
}
// 后手
public static int s(int[] arr, int i, int j) {
if (i=j) {
return 0;
}
return Math .min(f(arr, i + 1, j) //arr[i]
,f(arr, i, j - 1)); //arr[j]
}
动规
f作为一张表缓存
s作为一张表缓存
L>R时,数据无效,即数组左下半区无效
/pic:mw://2c14ddb958445ac6716418d6047774b8
public static int win2(int[] arr) {
//进行过滤
if (arr == nu11|I arr.length == 0) {
return 0;
}
int N=arr.length;
int [][]f=new int[N][N];
int [][]f=new int[N][N];
for(int i=0;i<N;i++){
// if(L==R){
// return arr[L];
//}
f[i][i]=arr[i];
//if (i=j) {
//return 0;
//}
s[i][i]=0;
}
for(inti=1;i<N;i++){
int L =0;
int R =i;
while(L<N&&R<N){
//f[row][col] = ?;
//return Math. max(arr[L]+ s(arr, L + 1, R),arr[R] + s(arr, L, R - 1));
f[L][R] = Math . max(
arr[L] + s[L + 1][ R],
arr[R] + s[L][R - 1]
);
//return Math .min(f(arr, i + 1, j) //arr[i] ,f(arr, i, j - 1)); //arr[j]
s[L][R] = Math.min(
f[L + 1][R], // arr[i]
f[L][R - 1] // arr[j]
);
L++;
R++;
}
}
//return Math . max(f(arr,0, arr.length - 1), s(arr, 0, arr .1ength - 1));
return Math.max(f[0][arr.length - 1]
,s[0][arr.length - 1]
);
}
拿钞票问题递归到动态规划
一个数组,里面的元素代表钞票面额,每种钞票都可以无穷次的拿,数组中无重复值、均为正数
给一个目标值,求用数组中有多少种办法将目标值凑出来?
// arr中都是正数且无重复值,返回组成aim的方法数
public static int ways(int[] arr, int aim) {
if(arr==nu1l||arr.1ength=0|1aim<0){
return 0;
}
return process(arr, 0, aim);
}
//可以自由使用arr[index... ]所有的面值,每一种面值都可以使用任意张,
//组成rest,有多少种方法
public static int process(int[] arr, int index, int rest) {
if(index == arr.1ength) {
return rest ==0?1 :0 ;
}
int ways = 0;
for(int zhang = 0;zhang * arr[index] <= rest ;zhang++) {
ways += process(arr, index + 1, rest - (zhang * arr[index]) );
}
return ways;
}
有重复过程,所以有必要优化
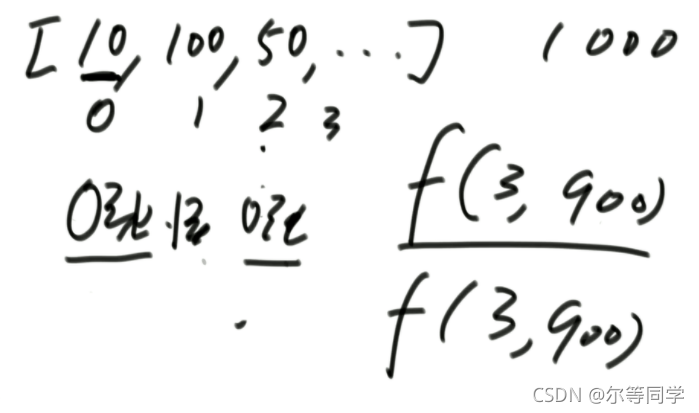
public static int ways2(int[] arr, int aim) {
if (arr == nu1l || arr .1ength == 0|1 aim < 0) {
return 0;
}
int[][] dp = new int[arr .1ength+1][aim+1];
//一开始所有的过程,都没有计算呢
// dp[..][..]
= -1
for(int i = 0 ; i < dp.1ength; i++) {
for(int j = 0 ; j < dp[8].1ength; j++) {
dp[i][j] = -1;
}
}
return process2(arr, 0,aim,dp);
}
//如果index和rest的参数组合,是没算过的,dp[index][rest]:== -1
//如果index和rest的参数组合,是算过的,dp[index][rest]> -1
public static int process(int[] arr, int index, int rest,int [][]dp) {
if(dp[index][rest] != -1) {
return dp[index][rest];
}
if(index == arr.1ength) {
dp[index][rest]=rest ==0?1 :0 ;
//return rest ==0?1 :0 ;
return dp[index][rest];
}
int ways = 0;
for(int zhang = 0;zhang * arr[index] <= rest ;zhang++) {
ways += process(arr, index + 1, rest - (zhang * arr[index]),dp );
}
// 进行缓存
dp[index][rest]=ways;
return ways;
}
动态规划
由下到上进行计算,每一行从左往右
public static int ways2(int[] arr, int aim) {
if (arr == nu1l || arr .1ength == 0|| aim < 0) {
return 0;
}
int N=arr.length;
int[][] dp = new int[N+1][aim+1];
//一开始所有的过程,都没有计算呢
// dp[..][..]= -1
//if(index == arr.1ength) {
// return rest ==0?1 :0 ;
//}
dp[N][0]=1;//dp[N][1...aim]=0;
for(int index = N - 1; index >= 0; index--) {
for(int rest = 0; rest <= aim; rest++) {
//dp[index][rest] = ?;
int ways = 0;
for(int zhang = 0;zhang * arr[index] <= rest ;zhang++) {
ways += dp[index + 1][rest - (zhang * arr[index])];
}
dp[index][rest] = ways;
}
}
return dp[0][aim];
}
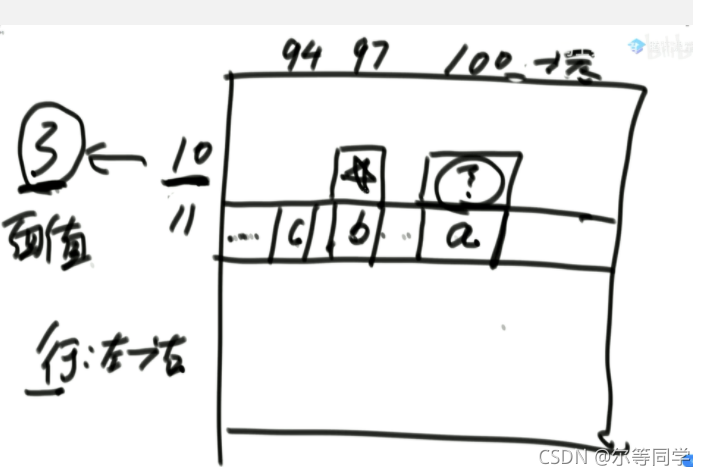
因为有枚举行为,可以进行优化
比如,f(3,100) 其实是依赖 f(3,97)的
public static int ways2(int[] arr, int aim) {
if (arr == nu1l || arr .1ength == 0|1 aim < 0) {
return 0;
}
int N=arr.length;
int[][] dp = new int[N+1][aim+1];
//一开始所有的过程,都没有计算呢
// dp[..][..]= -1
//if(index == arr.1ength) {
// return rest ==0?1 :0 ;
//}
dp[N][0]=1;//dp[N][1...aim]=0;
for(int index = N - 1; index >= 0; index--) {
for(int rest = 0; rest <= aim; rest++) {
//dp[index][rest] = ?;
dp[index][rest] = dp[index+1][rest];
if(rest-arr[index]>=0){
dp[index][rest]+=dp[index][rest-]
}
}
}
return dp[0][aim];
}
字符贴纸问题
给定一个字符串str,给定一个字符串类型的数组arr。
arr里的每一-个字符串, 代表一张贴纸, 你可以把单个字符剪开使用,目的是
拼出str来。
返回需要至少多少张贴纸可以完成这个任务。
例子: str= "babac",; a
arr = {"a",","abcd"}
至少需要两张贴纸"ba"和"abcd",因为使用这两张贴纸,把每-个字符单独剪
开,含有2个a、2个b、1个c。是可以拼出str的。所以返回2。
public static int minStickers1(String[] stickers, String target) {
int n = stickers. length;
int[][] map = new int[n][26];// stickers -> [26] [26] [26]
for(inti=0;i<n;i++){
char[] str = stickers[i]. toCharArray();
for (char C_ : str) {
map[i][c - 'a]++;
}
}
HashMap<String, Integer> dp = new HashMap<>();
dp.put("", 0);
return process1(dp, map, target);
}
// dp傻缓存,如果t已经算过了,直接返回dp中的值
// t剩余的目标
// 0..N每- .个字符串所含字符的词频统计
public static int process1(
HashMap<String, Integer> dp,
int[][] map,
String rest) {
if (dp. containsKey(rest)) {
return dp. get(rest);
}
//以下就是正式的递归调用过程
int ans = Integer .MAX_ VALUE; // ans ->搞定rest,使用的最少的贴纸数量
int n = map.1ength; // N种贴纸
int[] tmap = new int[26]; // tmap 去替代rest
char[] target = rest. toCharArray();
for (char C : target) {
tmap[c - 'a']++;
}
// map -> tmap
for(inti=0;i<n;i++){.
//枚举当前第--张贴纸是谁?|
if (map[i][target[0] - 'a'] == 0) {
continue;
}
StringBuilder sb = new StringBuilder();
//i贴纸,j枚举a~z字符
for(intj=0;j<26;j++){//
if (tmap[j] > 0) { // j这个字符是target需要的
for (int k = 0; k < Math.max(0, tmap[j] - map[i][j]); k++) {
sb. append((char) ('a'+ j));
}
}
//sb->i
String s = sb. toString();
int tmp = process1(dp, map, s);
if (tmp != -1) {
ans = Math.min(ans, 1 + tmp);
}
// ans 系统最大rest
dp. put(rest, ans == Integer .MAX_ .VALUE ? -1 : ans);
return dp.get(rest);
}
最长公共子序列问题
两个样本问题模型

情况1
最长公共子序列 不以str1 的最后一个字符结尾,也不以str2的最后一个字符结尾
情况2
最长公共子序列 以str1 。。。结尾,不以str2。。。结尾
情况3
情况2取反
情况4
情况1取反
public static int lcse(char[] str1, char[] str2) {
int[][] dp = new int[str1. length][str2.1ength];①
dp[0][0] = str1[0] == str2[0] ? 1 : 0;
for (int i = 1; i < str1.length; 1++) {
dp[i][0] = Math.max(dp[i - 1][0], str1[i] = str2[0] ? 1 : 0);
for (int j = 1; j < str2.1ength; j++) {
dp[0][j] = Math.max(dp[0][j - 1], str1[0] == str2[j] ? 1 : 0);
}
for (int i = 1; i < str1.1ength; i++) {
for (int j = 1; j < str2.1ength; j++) {
dp[i][j] = Math.max(dp[i - 1][i], dp[i][j - 1]);
if (str1[i] = str2[j]) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - 1] + 1);
}
}
}
return dp[str1.1ength - 1][str2.1ength - 1];
}
业务限制的尝试模型
给定一个数组,代表每个人喝完咖啡准备刷杯子的时间
只有一台咖啡机,一次只能洗一个杯子,时间耗费a,洗完才能洗下一杯
每个咖啡杯也可以自己挥发干净,时间耗费b,咖啡杯可以并行挥发
返回让所有咖啡杯变干净的最早完成时间
三个参数: int[] arr、 int a 、 int b
// process(drinks, 3,10, 0,0)
// a洗一杯的时间固定变量
// b自己挥发干净的时间固定变量
// drinks 每-一个员工喝完的时间固定变量
// drinks[0..index-1]都已经干净 了,不用你操心了
// drinks[index...]都想变 干净,这是我操心的,washLine 表示洗的机器何时可用
// drinks[index...j变干净, 最少的时间点返回
public static int process(int[] drinks, int a, int b,int index, int washLine) {
if (index == drinks.1ength - 1) {
return Math . min(
Math . max(washLine, drinks[index]) + a
, drinks[index] + b
);
//剩不止一杯咖啡
//wash是我当前的咖啡杯,洗完的时间
int wash = Math. max(washLine, drinks[index]) + a;// 洗,index- -杯,结束的时间点
// index+1...变干净的最早时间
int next1 = process(drinks, a, b,index + 1, wash);
// index...
int p1 = Math. max(wash, next1);
//剩不止一杯咖啡
//wash是我当前的咖啡杯,洗完的时间
int wash = Math. max(washLine, drinks[index]) + a;// 洗,index- -杯, 结束的时间点
// index+1... 变干净的最早时间
int next1 = process(drinks, a, b, index + 1, wash);
// index....
int p1 = Math . max(wash, next1);
int dry = drinks[index] + b; //挥发,index- -杯, 结束的时间点.
int next2 = process(drinks, a, b, index + 1, washLine);
int p2 = Math . max(dry, next2);
}
return Math.min(p1, p2);
}